回顾学习算法时所必须了解的一些基本知识。

本篇文章用于简要梳理在算法中的一些需要了解的基本知识点。

算法分析

To measure is to know. If you can not measure it, you can not improve it.

本部分通过引入理想、统一、分层次的尺度标准，来衡量算法的性能。

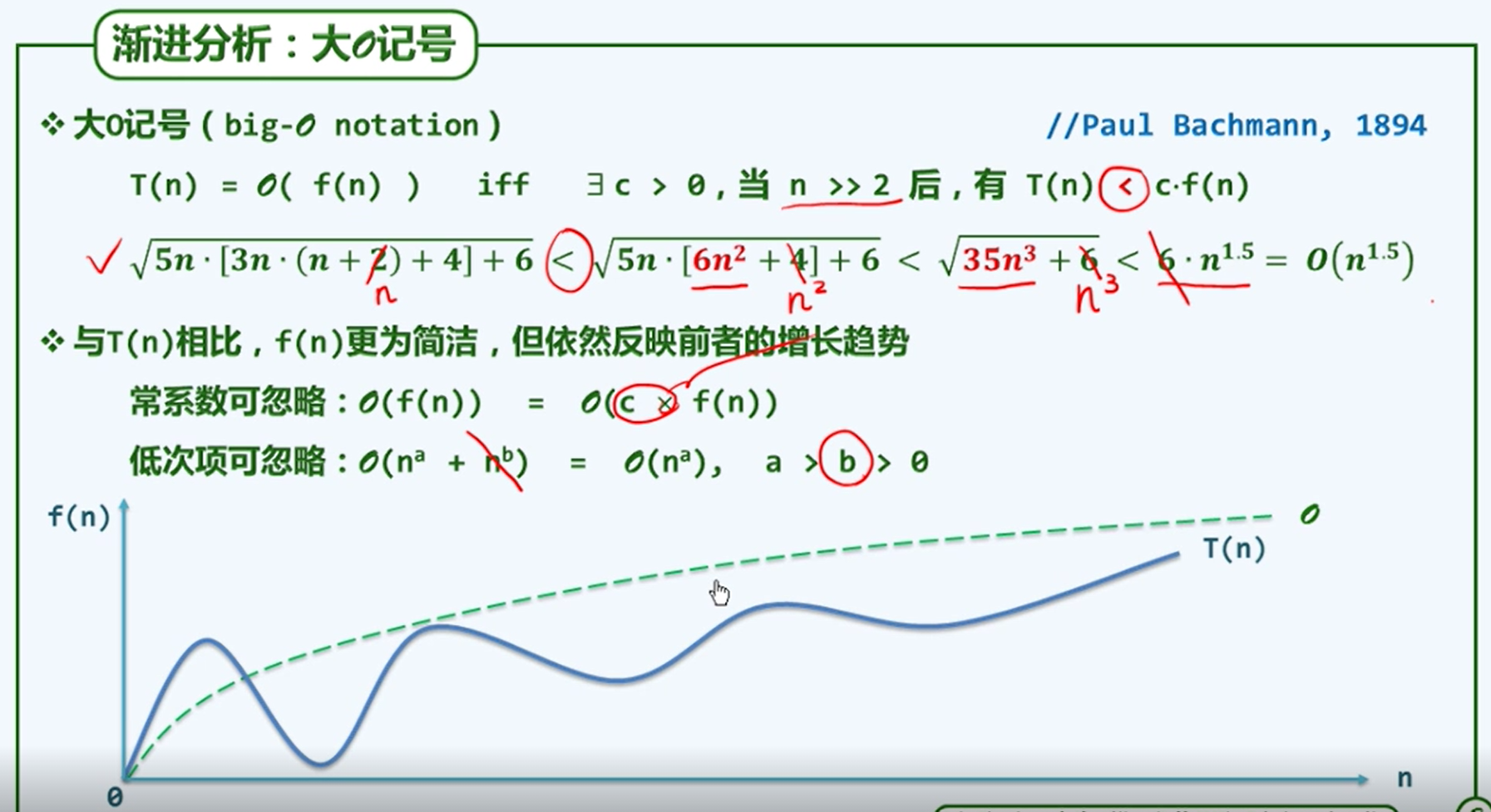
大O记号

大O记号通过划分上界，来悲观地衡量一个算法的性能。

注意：O(f(n)) 并不一定会完全处于 T(n) 之上，但可以通过如图中对 f(n) 乘以常系数 c 来做到拉高上界的作用。

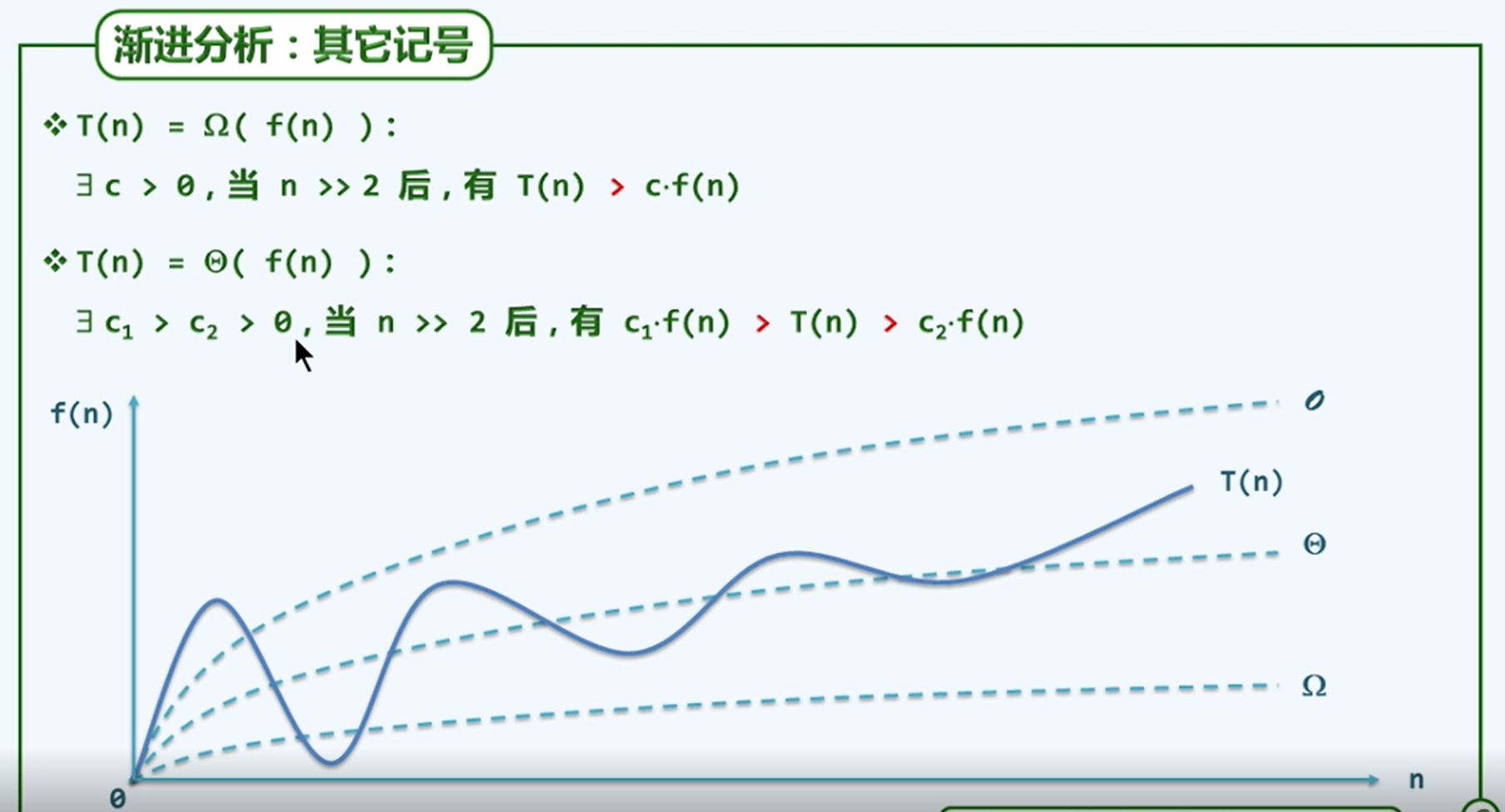
其它记号

大O记号的刻度

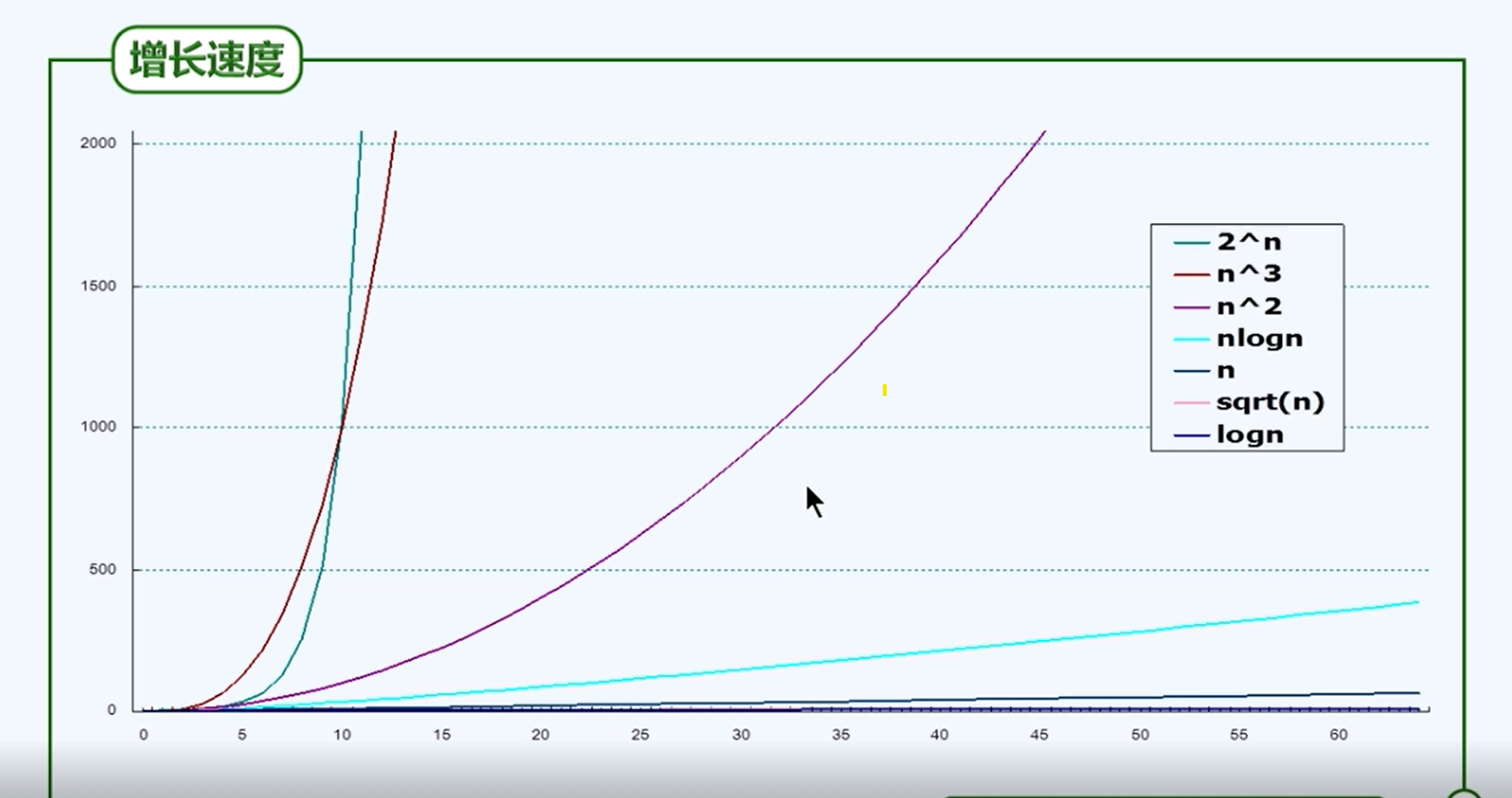
常数复杂度 O( 1 )

算法不含随输入规模变换的转向（循环、调用、递归等），且顺序执行，则说这个算法的复杂度为 O(1)。

对数复杂度 O( log^c(n) )

在此种情况中，对数的底数常常会被忽略，因为往往可以通过数学变换来改变对数的底数。

这类算法非常高效，复杂度无限接近于常数。

多项式复杂度 O( n^c )

此种复杂度由于影响因素往往取决于最高次幂项，因此较低次幂的项往往忽略不计。

其中，当幂次 c == 1 时，表示算法的时间复杂度与 n 线性相关，因此称 O(n) 为线性复杂度。

指数复杂度 O( 2^n )

当一个算法的计算成本按指数增长时，往往我们认为此种算法为问题的难解。

我们可以从下图中观察各个复杂度的增长速度：

级数

以下图片总结了一些常见的级数。